검정력 power
▶ 검정력(1−𝛽): 귀무가설이 거짓일 때 이를 올바르게 기각할 확률
- 유의수준 𝛼 : 귀무가설이 참일 때 기각하는 1 종 오류의 확률
- 𝛽: 귀무가설이 거짓일 때 기각하지 못하는 2 종 오류의 확률
- 보통 검정력은 0.8 이상을 요구
- 표본의 크기가 크면 증가
- 분석결과에 나오는 검정력은 모수가 통계량과 같다는 가정 아래 계산됨
- 참고수치.
t검정은 모수검정, 모수에 대한 여러 가정들이 존재.
-> 데이터가 많으면 이런 가정들을 충족, 문제 없음.
비모수 검정 방법 : 모수에 대해 특별한 가정을 안 함.
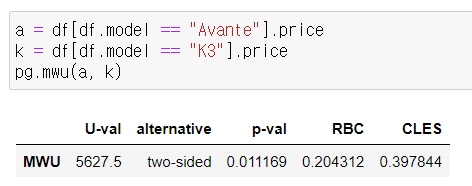
맨휘트니 U 검정 Mann Whitney U test
- 독립표본t 검정에 대응하는 비모수 검정 방법
- 귀무가설 두 집단의 모집단은 같다
- U 검정을 가끔 쓸 경우 : 연속형 변수가 아닌 경우
- ex) 순서형 변수, 서열형 변수
- ex) 학력 : 초절 < 중졸 < 고졸 < 대졸 < ...

에타제곱 = 1
▶ 집단 간 차이만 있고 집단 내 차이는 없음
실험 조건에 따라 모든 것이 달라짐
실험 조건이 같으면 결과도 같음
예) 대조군 데이터는 1, 1, 1 이고 실험군 데이터는 3, 3, 3 인 경우
에타제곱 0
▶ 집단 간 차이는 없고 집단 내 차이만 있음
실험조건에 따라 아무 것도 달라지지 않음
같은 실험 조건에도 서로 다름
예) 대조군 데이터는 1, 2, 3 이고 실험군 데이터도 1, 2, 3 인 경우

보통 언어로 표현한 효과 크기 CommonLanguage Effect Size (CLES)
- A, B 두 집단에서 무작위로 값을 하나씩 뽑았을 때
- A집단에서 뽑힌 값이 B 집단에서 뽑힌 값보다 클 확률
연식: 여러 가지 값을 가지는 경우 t-test: 2 집단을 비교하는 방법 연식을 임의로 2집단으로 나눠서 비교할 수는 있음 별로 좋지는 않음(왜 2014년이죠?) 1) 두 집단으로 나누는 기준이 임의적 2) 분포가 왜곡될 수 있음(t-test의 가정과 잘 맞지 않게 될 수 있음)
두 집단 비교
t-test : 귀무가설 : 두 집단의 평균이 같다(차이가 없다)
p < 0.05 => 귀무가설 기각 => 다르긴 다르다.
얼마나 다른데 ? => 효과 크기(에타제곱, Cohen's d)
U-test : 둘이 다르다 => 크기순으로 늘어놓으면 골고루 섞임
p < 0.05 => 귀무가설 기각 => 둘이 다르긴 다르다. 얼마나 다른데? => 효과 크기(CLES)
대응표본 paired samples
▶ 대응표본 : 두 집단의 자료를 쌍으로 묶을 수 있을 때
예) 남편과 아내 , 쌍둥이 , before & after
▶ 두집단의 자료를 쌍으로 묶어야 하기 때문에 , 독립표본과는 달리 두 집단의 자료 갯수가 동일해야 함
- • 독립표본t 검정 : 평균의 차이를 비교
• 대응표본t 검정 : 차이의 평균을 비교
| 평균 | 비모수 | |
| 독립표본 | t-test | mwu |
| 대응표본 | t-test (paired=True) | wilconxon |

분산분석 Analysis of Variance
- 집단 간 차이가 크다면 집단 내 분산 에 비해 집단 간 분산 이 커질 것
- 모집단이 정규 분포를 따르거나 각 집단의 표본 크기가 충분히 크면
- -> 집단간 분산 집단 내 분산의 비율은 F 분포를 따름
- F = (집단 간 차이) / (집단 내 차이)
- 이를 통해 '모든 집단들의 평균이 같다' 는 귀무가설을 검정할 수 있음
- 귀무가설을 기각할 경우 '적어도 한 집단의 평균은 다르다' 라는 대립 가설을 채택
등분산성 homoscedasticity
- 분산분석은 집단간 분산이 같아야 함
- 등분산성은 Levene 검정으로 확인할 수 있음
- 귀무가설 집단 간 분산이 같다
- p < 유의수준 → 귀무가설 기각 → 집단 간 분산이 다름
- 집단 간 분산이 다를 경우(이분산) 별도의 보정이 필요
사후검정 post hoc test
- FWER을 통제하기 위해 분산 분석을 먼저 실시
- 분산 분석 결과가 통계적으로 유의하면 𝑝<𝛼 사후 검정을 실시
- 여러 집단 중 통계적으로 유의한 차이가 나는 집단을 식별
- 사후 검정에서도 𝛼를 조절하여 FWER 이 커지지 않도록 제어
- 각 집단의 분산이 같은 경우 Tukey HSD
- 각 집단의 분산이 다른 경우 Games Howell 검정
FWER Familywise Error Rate
- 다중 비교를 할 경우 적어도 한 번 1 종 오류가 발생할 확률
- 비교를 많이 할 수록 FWER 은 증가
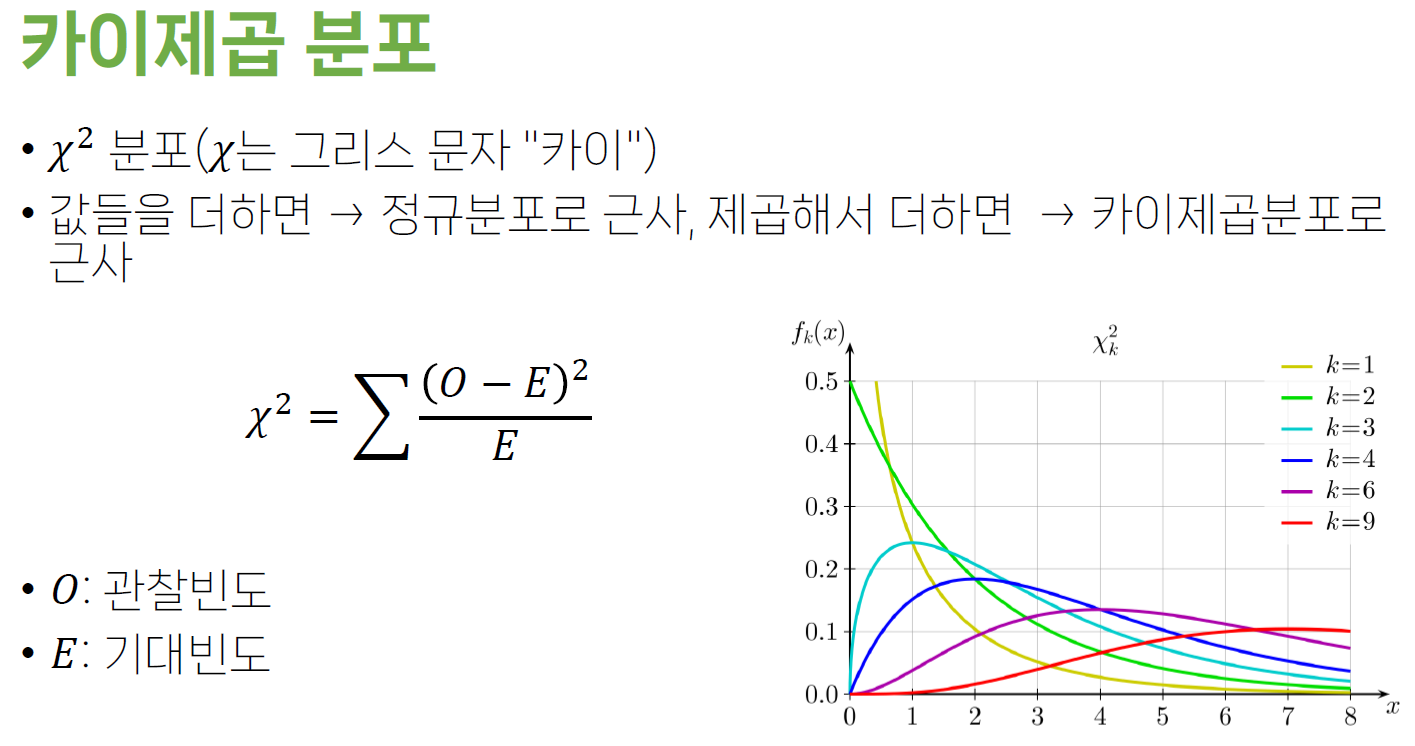
카이제곱 적합도 검증 chi square test for goodness of fit
• 표본에서 얻은 분포가 귀무가설에서 가정하는 모집단 분포와 잘 맞는지(goodness of fit)를 알아보기 위해 사용
• 귀무가설 : 모집단에서 비율은 기대빈도의 비율과 같다
- 예 : 브랜드 선호도
- 50명을 대상으로 설문했을 때 A 브랜드를 선호하는 고객 은 31 명 (62%), B 브랜드를 선호하는 고객은 19 명 ( 38%)
- → A 브랜드에 대한 선호도가 통계적으로 유의하게 높은가?
- 100명을 대상으로 설문했을 때 A 브랜드를 선호하는 고객 은 62 명 (62%), B 브랜드를 선호하는 고객은 38 명 ( 38%)
- → A 브랜드에 대한 선호도가 통계적으로유의하게 높은가?

카이제곱 독립성 검증 chi square test for independence
카이제곱 독립성 검증은 두 범주 변수 간에 관계가 있는지 알아보기 위해 사용
귀무가설 : 두 변수가 독립적이다 (= 관계가 없다.)
※ 카이제곱독립성 검증은 모든 셀의 기대값이 5 혹은 그 이상이라는 가정에 기반.
- 예시)
- 남녀간의 브랜드 선호도 차이
- 지역별 정당 지지율에 차이
- 혈액형과성격유형의 관계
데이터가적으면 p value 가 부정확할 수 있음
▶ 모든 기대빈도가 5 혹은 그 이상이어야 함
Cramé r's V: 두 변수의 관계를 0~1 로 표시
- 0:전혀 관련이 없음
- 1:완전히 일치

'멋쟁이사자처럼 AI School 8기(fin) > TIL(Today I Learn)' 카테고리의 다른 글
| [멋쟁이사자처럼 AI스쿨] Day36 - TIL with 통계 (0) | 2023.02.17 |
|---|---|
| [멋쟁이사자처럼 AI스쿨] Day35 - TIL with 통계 (0) | 2023.02.16 |
| [멋쟁이사자처럼 AI스쿨] Day33 - TIL with 통계 (0) | 2023.02.14 |
| [멋쟁이사자처럼 AI스쿨] Day32 - TIL, 통계학 week with(유재명) (1) | 2023.02.13 |
| [멋쟁이사자처럼 AI스쿨] Day-30 TIL (0) | 2023.02.08 |


